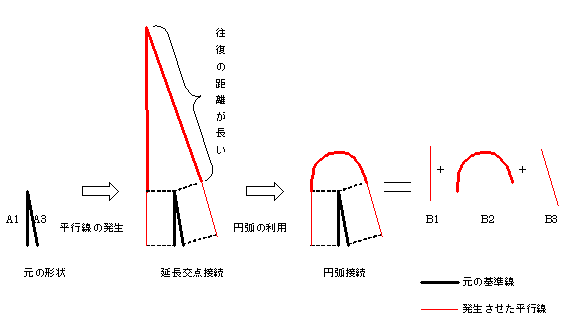
それならば、図 3の場合はどうでしょう。この時、図 2の「接続後の平行線」で導入した、単純に交わるまで延長する手法だと、図 3の様に鋭い鋭角で接続する場合、問題が発生します。まず、交点までの延長距離が図 3より明らかな通り、極めて大きくなります。結果として、発生させた平行線が元の形状からかなり離れてしまうことになるのですが、これは許されるのでしょうか。

そもそも平行線とは何かを考えた時に、元の基準線分からの距離が一定である点の軌跡ではないでしょうか。とすると、図 3の「延長交点接続」の様に距離的に著しく元の基準線から乖離した平行線を作ることは宜しくないことが分かります。

とすると答えとして、図 3の「円弧接続」の様に、基準線の接続点を中心とする円弧でつなぐ方法を考え付きます。

さて、この円弧でつなぐ方法についてもうちょっと考えてみると、結局、図 3の右端に示す通り、出来上がった平行線は、B1、B2、B3の３つの部分から構成されていることが分かります。ここで、B1、B3は元の基準線分のA1、A3にそのまま対応します。そしてB2はA1とA3の接続点（この接続点は、基準線の方向変化点とも考えられますね）に対応していることが分かります。さて、この接続点における円弧B2の形状は当然その前後の線分A1、A3の方向、別の言い方をすると線分列の接続状況によって変わります。と言うことは、平行線の発生の際には、個別の線分に対する平行線を考えるだけでは十分でなく、その間のつなぎ方を、元の基準線分列の一種の流れ、方向性を考慮して、考えなければいけないのです。そしてこれが、平行線発生が単純に行かない理由を一言で表現する言い方だと弊社は考えています。